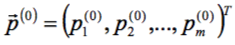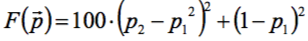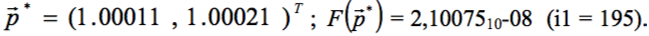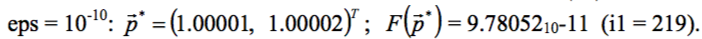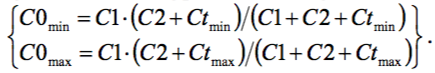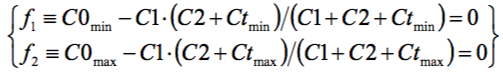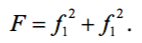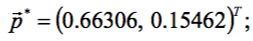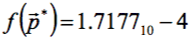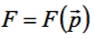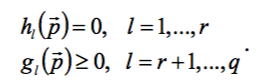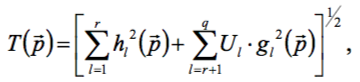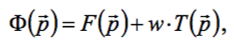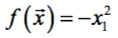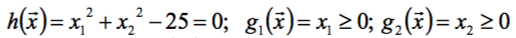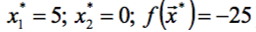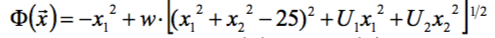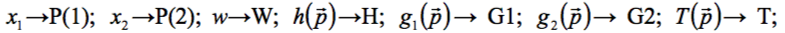Программа минимизации функции многих переменных методом деформируемого многогранника (по Нелдеру и Миду)
Реализован алгоритм минимизации функции многих переменных без вычисления производных. В основу положен метод деформируемого многогранника, известный также как модифицированный симплекс-метод. Программа ("Simplex") написана на языке Excel Vusual Basic и опубликована в сети Интернет для свободного пользования.
Предлагается в качестве простого и эффективного средства решения широкого круга вычислительных задач, таких как: решение линейных и нелинейных уравнений и их систем, минимизация суммы квадратов для линейных и нелинейных регрессий, поиск экстремумов функций без ограничений и с ограничениями в виде равенств и неравенств и т.п. Описан алгоритм и порядок использования программы, дан ряд примеров решения наиболее типичных задач.
Алгоритм метода деформируемого многогранника (модифицированный симплекс-метод) для минимизации функции многих переменных был предложен Нелдером и Мидом в 1964 г. [1]. Вошёл во многие учебники, монографии и курсы по прикладным математическим методам. Алгоритм метода на ЭВМ реализовывался неоднократно, например, в монографии [2] он представлен на языке Fortran IV (предложенный программный код не оптимален (содержит избыточные обращения к процедуре вычисления функции, может быть сокращен). Зарекомендовал себя как довольно надёжный инструмент в инженерных расчётах, связанных с минимизацией функций многих переменных с ограничениями и без. В настоящей работе алгоритм рассмотрен по возможности подробно и представлен в виде программы-макроса "Simplex" на внутреннем языке VBA (Visual Basic for Applications) популярного приложения MS Office Excel для ПК, оснащённых ОС Windows. Особое внимание уделено рассмотрению конкретных примеров использования программы.
Постановка задачи и суть рассматриваемого метода в упрощенном изложении сводится к следующему.
Имеется целевая функция (ЦФ): 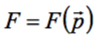 , где
, где 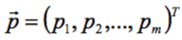 − вектор (набор) её параметров (T – знак транспонирования – замены строки на столбец; вектор является столбцом). Требуется найти такое значение вектора,
− вектор (набор) её параметров (T – знак транспонирования – замены строки на столбец; вектор является столбцом). Требуется найти такое значение вектора, 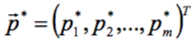 , при котором F принимает минимальное значение:
, при котором F принимает минимальное значение: 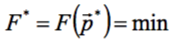 . Для этого в пространстве параметров и целевой функции размерности m + 1 из некоторой начальной точки
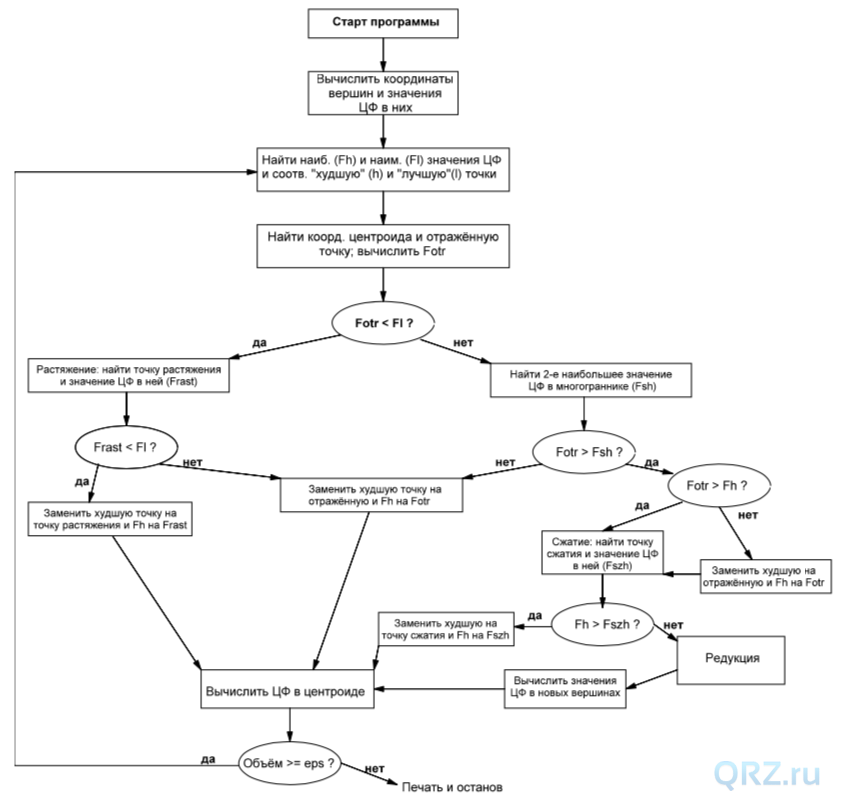
. Для этого в пространстве параметров и целевой функции размерности m + 1 из некоторой начальной точки 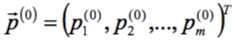 строится по определённым правилам равносторонний (изначально) многогранник, называемый симплексом, длина рёбер которого определяется шагом симплекса s. В m + 1 вершинах симплекса вычисляются значения F. Далее эти значения сравниваются и выбираются 2 вершины – лучшая и худшая – где значения F, соответственно, наименьшее и наибольшее. Для оценки направления, в котором функция уменьшается, производится отражение худшей вершины относительно центроида многогранника. Если в отражённой точке значение F получилось ещё меньше, производится операция растяжения симплекса. Всякий раз при удачном шаге координаты худшей точки заменяется координатами вновь найденной лучшей. При неудачных шагах, т.е. когда не удаётся найти точки, где F меньше, чем уже было достигнуто, предусмотрен поиск второго большего значения, а также сжатие симплекса по текущему направлению и его редукция – уменьшение всех сторон многогранника. В целом, по мере продвижения к минимуму F, многогранник изменяет свою конфигурацию, приспосабливаясь к топологии гиперповерхности ЦФ, а в окрестностях самого минимума уменьшает свой объём до некоторой заданной предельной величины ε . Когда это происходит, считается, что минимум F найден. Более детально алгоритм метода и программы представлен в виде блок-схемы на рис. 1.
строится по определённым правилам равносторонний (изначально) многогранник, называемый симплексом, длина рёбер которого определяется шагом симплекса s. В m + 1 вершинах симплекса вычисляются значения F. Далее эти значения сравниваются и выбираются 2 вершины – лучшая и худшая – где значения F, соответственно, наименьшее и наибольшее. Для оценки направления, в котором функция уменьшается, производится отражение худшей вершины относительно центроида многогранника. Если в отражённой точке значение F получилось ещё меньше, производится операция растяжения симплекса. Всякий раз при удачном шаге координаты худшей точки заменяется координатами вновь найденной лучшей. При неудачных шагах, т.е. когда не удаётся найти точки, где F меньше, чем уже было достигнуто, предусмотрен поиск второго большего значения, а также сжатие симплекса по текущему направлению и его редукция – уменьшение всех сторон многогранника. В целом, по мере продвижения к минимуму F, многогранник изменяет свою конфигурацию, приспосабливаясь к топологии гиперповерхности ЦФ, а в окрестностях самого минимума уменьшает свой объём до некоторой заданной предельной величины ε . Когда это происходит, считается, что минимум F найден. Более детально алгоритм метода и программы представлен в виде блок-схемы на рис. 1.
Идентификаторы программы.
а) целые (integer):
m – размерность вектора (число) параметров ЦФ;
n – число точек регрессии (когда программа используется как МНК);
i1 – количество вычислений ЦФ;
L – номер вершины многогранника, в которой значение ЦФ минимально;
H – то же, где оно максимально;
i, j, k, u – индексы; k1, k2, k3, k4 – вспомогательные;
б) константы:
alfa – коэффициент отражения; beta – коэффициент сжатия; gamma –
коэффициент растяжения; step – величина шага; eps – минимальный объём
многогранника; d1, d2 – вспомогательные;
в) переменные:
F2 – целевая функция, ЦФ; F1 – функция-модель (используется в случае МНК);
S1 – второе наибольшее значение ЦФ в многограннике; C1 – вспомогательная;
mnk – логическая переменная (Boolean), имеющая значения: True. когда
программа используется как МНК, иначе – False;
г) массивы:
P(1 to m) – вектор параметров ЦФ;
X(1 to n) – массив независимой переменной (абсцисса регрессии) в МНК;
Y(1 to n) – массив наблюдений (ордината регрессии) в МНК;
S(1 to m + 4, 1 to m) – массив координат вершин и точек многогранника;
F(1 to m + 4) – массив значений ЦФ в вершинах и точках многогранника.
Структура массива величин S(i , j) следующая:
индексы принимают значения: i = 1, …, m + 4; j = 1, …, m.
S(1, j) – координаты исходной точки 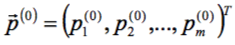
от S(2 ,j) до S(m +1, j) – координаты вершин симплекса;
S(m + 2, j) – координаты центроида;
S(m + 3, j) – отражённая точка;
S(m + 4, j) – точка растяжения или сжатия.
Порядок пользования программой.
Программа написана на языке Basic в среде VBA (Visual Basic for Applications). Это встроенный язык программирования Excel в пакете MS Office [3]. Для использования программы, необходимо, чтобы на ПК, оснащённом ОС MS Windows XP или более поздней, было установлено приложение MS Office Excel (Следующее относится к Excel 2003).
Проделать следующее:
- Скачать и сохранить файл программы simplex.xls, пройдя по ссылке [4].
- Открыть приложение Excel, не открывая скачанного файла.
- Т.к. программа является макросом, необходимо снизить уровень безопасности приложения, для чего войти в основном меню по пути: Сервис > Макрос > Безопасность; на открывшейся вкладке выбрать средний уровень безопасности.
- Открыть файл программы и в открывшемся окне предупреждения системы безопасности выбрать «Не отключать макросы». Появится главное окнопрограммы – "Simplex".
Кроме того, имеются ещё две вкладки: "Константы" и "МНК". Из констант следует ввести во второй столбец: "число параметров минимизируемой функции, m" и "используется ли Simplex как МНК (True или False)". В случае МНК нужно ввести также число точек регрессии, n. Прочие константы установлены по умолчанию и их можно не менять. На вкладке "МНК" размещается регрессионная таблица, где в соответствующем случае заполняются столбцы X(u) и Y(u), согласно заданной величине n (1-ый столбец можно не заполнять).
Для просмотра программного кода и занесения необходимых описаний конкретных функций надо пройти из основного меню по пути: Сервис > Макрос > Редактор Visual Basic либо нажать <Alt+F11>. Откроется окно Microsoft Visual Basic – simplex.xls с текстом программы (Если данное окно пустое, то из его главного меню пройти: View > Project Explorer (или нажать <Ctrl + r>) и в открывшемся окошке Project-VBAProject дважды щёлкнуть на Module1.).
Примечание:
в Excel 2010 для запуска редактора Visual Basic необходимо перейти на вкладку "Разработчик" и в группе Код нажать кнопку Visual Basic: откроется интегрированная среда разработки приложений Visual Basic. Если на ленте в Microsoft Office Excel 2010 нет вкладки "Разработчик", необходимо выполнить следующие действия: 1. Перейти на вкладку Файл и нажать на кнопку Параметры. 2. В открывшемся окне Параметры Excel выбрать слева категорию "Настройка ленты", а справа в группе "Настройка ленты" в раскрывающемся списке "Основные вкладки" установить флажок "Разработчик" и нажать на кнопку ОК. Для быстрого запуска редактора VBA достаточно нажать комбинацию клавиш <Alt+F11>.
Программа составлена из следующих процедур (Subroutines):
- Sub Simplex() − собственно программа симлекс-метода по Нелдеру и Миду.
- Sub OF() − процедура вычисления ЦФ, F2 (Objective Function).
- Sub MF(u) – процедура вычисления функции-модели F1 в МНК (Model Function), где u – зарезервированный индекс (public integer), относящийся к u-ой точке регрессии. Важное замечание: индексы i, j также являются зарезервированными (для массивов S и F), и применять их в процедурах для функций не следует.
- Sub RS() – процедура восстановления симплекса (Restore Simplex); применяется в случае непредвиденного коллапса многогранника; о ней будет сказано в конце статьи.
Дальнейший порядок работы с программой лучше всего рассмотреть на конкретных примерах.
1о. Минимизация функции без ограничений.
Найти минимум функции 2-х переменных:
Это т.н. функция Розенброка, отличающаяся тем, что в пространстве параметров в области своего минимума 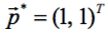 представляет собой узкий искривлённый овраг. Задача минимизации овражистых функций особенно затруднительна. Поэтому функцию Розенброка обычно используют как тестовую задачу в оценках эффективности тех или иных методов минимизации. Записываем процедуру вычисления ЦФ в виде (
представляет собой узкий искривлённый овраг. Задача минимизации овражистых функций особенно затруднительна. Поэтому функцию Розенброка обычно используют как тестовую задачу в оценках эффективности тех или иных методов минимизации. Записываем процедуру вычисления ЦФ в виде (В программе по умолчанию Sub OF( ) записана в более общем виде.
):
Sub OF() 'функция Розенброка
F2 = 100 * (P(2) - P(1) ^ 2) ^ 2 + (1 - P(1)) ^ 2
i1 = i1 + 1
End Sub
Примечание: последний оператор служит для подсчёта количества обращений к процедуре.
На вкладке "Константы" в соответствующие ячейки вводим: m → 2; mnk → False.
На вкладке "Simplex" вводим начальное приближение (в данном примере оно м.б. любым), например, нули.
Запускаем программу нажатием <Ctrl+s>. При заданной величине eps = 10-8 получаем результат:
При 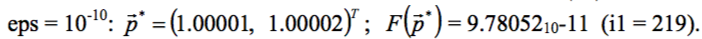
2о. Решение системы 2-х нелинейных уравнений.
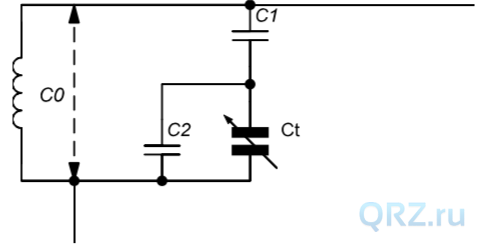
Рассмотрим такую практическую задачу. Необходимо рассчитать ёмкости растягивающих конденсаторов С1 и С2 колебательного контура (рис. 2), так чтобы при перестройке конденсатора переменной ёмкости от Ctmin до Ctmax ёмкость триады менялась в пределах от C0min до C0max.
Рис. 2. К расчёту конденсаторов растяжки.
4 В программе по умолчанию Sub OF( ) записана в более общем виде.
Имеем систему двух нелинейных уравнений с двумя неизвестными С1 и С2:
Вместо того, чтобы решать её алгебраическим путём (исключением одного неизвестного и сведением к квадратному уравнению для другого неизвестного), при неизбежных громоздких выкладках, применим программу "Simplex".
Перепишем систему так:
и зададим ЦФ в виде:
Ясно, что F равна нулю тогда и только тогда, когда оба слагаемых равны нулю, т.е. совокупность параметров С1 и С2, при которых значение F минимально, и будет решением задачи. Пусть конкретно (в пФ): Ctmin = 10; Ctmax = 500; C0min = 60; C0max = 200.
Обозначаем С1→P(1); С2→P(2). Процедура вычисления ЦФ будет выглядеть так:
Sub OF()
F2 = (60 - P(1) * (P(2) + 10) / (P(1) + P(2) + 10)) ^ 2
F2 = F2 + (200 - P(1) * (P(2) + 500) / (P(1) + P(2) + 500)) ^ 2
i1 = i1 + 1
End Sub
Запускаем программу и получаем (при старте из начала координат, округлённо): С1 = 310пФ; С2 = 64 пФ; значение ЦФ в минимуме = 1.7410-8 ; i1 = 175.
30. Использование программы в качестве МНК. Линейная регрессия.
Программа "Simplex" легко решает задачи минимизации суммы квадратов отклонений для линейных и нелинейных регрессий. В отличие от методов с производными, она устойчива и относительно нетребовательна к выбору начального приближения даже в случае сложных нелинейных моделей. Важно лишь не попасть в ложный (локальный) минимум, если таковой существует. Кроме того, чтобы не происходило арифметических авостов при наличии таких функций как показательная, квадратный корень, логарифм и т.п., надо позаботиться, чтобы переменные не выходили из области допустимых значений. И даже в этом случае можно применить программу в варианте минимизации с ограничениями (см. пример ниже). Недостатком методов без производных является то, что без специальных приемов с их помощью возможно лишь точечное оценивание параметров, т.е. без оценки их достоверности.
Рассмотрим линейную регрессию вида y(x) = ax + b, где x – независимая переменная, y(x) – наблюдения, a и b – оцениваемые параметры. Исходные данные
представлены в табл. 1.
Табл. 1. Линейная регрессия, исходные данные.
Заносим на вкладке «Константы» m→2; n→10; mnk→True. На вкладке "МНК" заполняем второй и третий столбцы регрессионной таблицы. Н вкладке "Simplex" начальное приближение – любое. Записываем процедуры, приняв, что a→P(1); b→P(2); x(u) →X(u);
y(u) →Y(u); y(x) →F1:
Sub OF()
F2 = 0
For u = 1 To n: Call MF(u): F2 = F2 + (Y(u) - F1) ^ 2: Next u
i1 = i1 + 1
End Sub
Sub MF(u)
F1 = P(1) * X(u) + P(2)
End Sub
Запускаем макрос и получаем из точки (0, 0)T оценки: 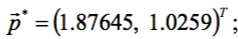 i1 =102. Открываем вкладку "МНК" и просматриваем результат подгонки регрессии.
i1 =102. Открываем вкладку "МНК" и просматриваем результат подгонки регрессии.
40. Использование программы в качестве МНК. Нелинейная регрессия.
В случае нелинейных регрессий порядок действий остаётся прежним, изменяются лишь: запись функции-модели в Sub MF(u), константы m и n, числа в регрессионной таблице.
Пусть требуется найти МНК-оценки параметров двухстадийной химической реакции типа A → B → C. Функция-модель для описания зависимости концентрации
промежуточного продукта от времени x имеет вид (Этот пример заимствован из [2], задача 3.44.):
Исходные данные для расчёта следующие (табл.2):
Табл. 2. Нелинейная регрессия, исходные данные.
Записываем процедуру для функции-модели, приняв, что p1→P(1); p2→P(2); xu →X(u); yu→Y(u); y →F1:
Sub MF(u)
F1 = P(1) / (P(1) - P(2)) * (Exp(-P(2) * X(u)) - Exp(-P(1) * X(u)))
End Sub
Для Sub OF() запись остаётся прежней, как в предыдущем примере. В качестве констант вводим: m → 2; n → 3; mnk → True. Начальные оценки разумно взять (2,1)T. Заметим, что нельзя выбирать одинаковые, равно и нулевые значения для начальных оценок обоих параметров. Запускаем макрос и получаем:
50. Минимизация функции с ограничениями.
Этот класс задач в прикладном нелинейном программировании считается самым сложным [2]. Однако программа "Simplex", как показал опыт, в большинстве случаев неплохо с ними справляется. Рассмотрим одну такую задачу, при этом воспользуемся приёмом, известным как метод штрафных функций (Penalty Functions).
Пусть требуется найти минимум функции 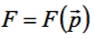 при наличии следующих условий (ограничений):
при наличии следующих условий (ограничений):
Определяется "штраф" к 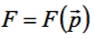 как мера невыполнения поставленных условий:
как мера невыполнения поставленных условий:
где Ul − т.н. оператор Хэвисайда, такой, что он равен 1, если условие 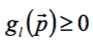 нарушено, и равен 0 в противном случае. Решение задачи сводится к минимизации штрафной функции (ШФ) вида
нарушено, и равен 0 в противном случае. Решение задачи сводится к минимизации штрафной функции (ШФ) вида
где w – вес штрафа. Чем больше величина w, тем больше требования к выполнению ограничений, но одновременно поиск минимума всё более осложняется из-за роста "овражности" функции. Поэтому процедуру минимизации осуществляют поэтапно: сначала находят минимум ШФ при w = 1, потом вес увеличивают, например, в 10 раз и находят уточнённый минимум, и т.д. до получения сходящихся результатов.
Для примера рассмотрим следующую задачу.
Найти минимум функции 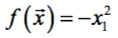 при следующих ограничениях:
при следующих ограничениях:
(правильный ответ: 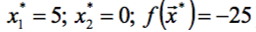 ).
).
Задаём ЦФ в виде штрафной функции:
Принимаем: 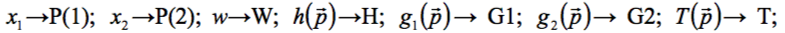
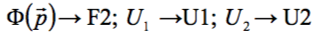
и записываем процедуру в следующем виде:
Sub OF()
’объявляем дополнительные переменные:
Dim H, G1, G2, T As Double, W As Single, U1, U2 As Integer
H = P(1) ^ 2 + P(2) ^ 2 - 25
G1 = P(1): G2 = P(2)
If G1 < 0 Then U1 = 1 Else U1 = 0
If G2 < 0 Then U2 = 1 Else U2 = 0
W = 1
T = Sqr(H ^ 2 + U1 * G1 ^ 2 + U2 * G2 ^ 2)
F2 = -P(1) ^ 2 + W * T
i1 = i1 + 1
End Sub
Результаты вычислений при разных весах штрафа и старте всякий раз из точки (0, 0)T приведены в табл. 3.
Табл. 3. Результаты минимизации функции с ограничениями.
|
|
Достигнутые значения в точке минимума
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Видно, что объём вычислений резко увеличивается по мере роста W, но уже при W=10 получается вполне точный результат.
60. Задача большой размерности.
Известно, что по мере увеличения размерности ЦФ (роста числа её параметров) поиск экстремумов всё более и более усложняется, и это происходит не только потому, что естественно увеличивается объём вычислений, но и начинают проявляться различные недостатки алгоритмов (т.н. "проклятие размерности").
Не лишён, по-видимому, недостатков и алгоритм Нелдера-Мида. Вот, например, как это проявляется на ЦФ вида:
для которой 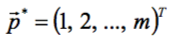
При m ≤ 4 и старте из начала координат поиск минимума не вызывает затруднений, однако уже при m = 5 процедура "выклинивается", не достигнув минимума. Анализ данного случая показал, что подобное непредвиденное окончание процедуры происходит из-за коллапса деформируемого многогранника, центроид которого попадает в самое русло оврага или очень близко к нему, а прочие точки расположились "неудачно"; тогда операции сжатия или редукции не приводят к успеху, т.к. лучшей точки всё равно не находится. Только при замене начальной точки на достигнутую и запуска программы "с нуля", ответ получается правильным. При m = 6 ситуация ещё больше усложняется и начальное приближение приходится заменять дважды (см. табл. 4).
Именно для данного случая предусмотрена процедура Sub RS(), упоминавшаяся выше. При её запуске (<Ctrl+r>) координаты достигнутого (предположительно ложного) минимума переписываются в ячейки начального приближения, и автоматически запускается Sub Siplex(). Так удаётся решить рассматриваемую задачу и при m = 7.
Правильный результат достигается за 4 прогона минимизации (табл. 5).
Табл. 4. Минимизация функции (#); m = 6.
|
|
Достигнутая точка (округлённо)
|
Достигнутое значение ЦФ F*
|
|
|
|
(0.71, -0.11, 5.1, 1.4, 2.7, 3.4)Т
|
|
|
|
|
(1.67, 2.2, 2.9, 3.9, 5.0, 6.1)Т
|
|
|
|
|
точный до 6-го знака ответ
|
|
|
Табл. 5. Минимизация функции (#); m = 7.
Т.о. в случае ЦФ большой размерности к результату, полученному за одну попытку (прогон), следует отнестись с осторожностью и убедиться, путём варьирования начального приближения, не найден ли локальный экстремум. Полезно также запуском процедуры Sub RS() выяснить, не "выклинилась" ли программа из-за коллапса многогранника.
Литература
- Nelder J.A., Mead R. // Computer Journal. – 1964. – V. 7. – P. 308.
- Химмельблау Д. Прикладное нелинейное программирование. – М.: Мир, 1975. 534 с.
- Э. Бунин. Excel Visual Basic для приложений (серия "Без проблем!"): Пер. с англ. – М.: Восточная Книжная Компания, 1966. – 352 с.
- URL: http://tsibanoff.narod.ru/algorythms/simplex.xls. Посещен 27.10.2017.
Комментарии
Оставьте свое мнение
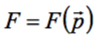 , где
, где 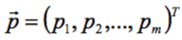 − вектор (набор) её параметров (T – знак транспонирования – замены строки на столбец; вектор является столбцом). Требуется найти такое значение вектора,
− вектор (набор) её параметров (T – знак транспонирования – замены строки на столбец; вектор является столбцом). Требуется найти такое значение вектора, 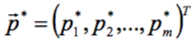 , при котором F принимает минимальное значение:
, при котором F принимает минимальное значение: 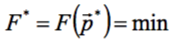 . Для этого в пространстве параметров и целевой функции размерности m + 1 из некоторой начальной точки
. Для этого в пространстве параметров и целевой функции размерности m + 1 из некоторой начальной точки 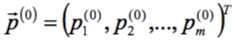 строится по определённым правилам равносторонний (изначально) многогранник, называемый симплексом, длина рёбер которого определяется шагом симплекса s. В m + 1 вершинах симплекса вычисляются значения F. Далее эти значения сравниваются и выбираются 2 вершины – лучшая и худшая – где значения F, соответственно, наименьшее и наибольшее. Для оценки направления, в котором функция уменьшается, производится отражение худшей вершины относительно центроида многогранника. Если в отражённой точке значение F получилось ещё меньше, производится операция растяжения симплекса. Всякий раз при удачном шаге координаты худшей точки заменяется координатами вновь найденной лучшей. При неудачных шагах, т.е. когда не удаётся найти точки, где F меньше, чем уже было достигнуто, предусмотрен поиск второго большего значения, а также сжатие симплекса по текущему направлению и его редукция – уменьшение всех сторон многогранника. В целом, по мере продвижения к минимуму F, многогранник изменяет свою конфигурацию, приспосабливаясь к топологии гиперповерхности ЦФ, а в окрестностях самого минимума уменьшает свой объём до некоторой заданной предельной величины ε . Когда это происходит, считается, что минимум F найден. Более детально алгоритм метода и программы представлен в виде блок-схемы на рис. 1.
строится по определённым правилам равносторонний (изначально) многогранник, называемый симплексом, длина рёбер которого определяется шагом симплекса s. В m + 1 вершинах симплекса вычисляются значения F. Далее эти значения сравниваются и выбираются 2 вершины – лучшая и худшая – где значения F, соответственно, наименьшее и наибольшее. Для оценки направления, в котором функция уменьшается, производится отражение худшей вершины относительно центроида многогранника. Если в отражённой точке значение F получилось ещё меньше, производится операция растяжения симплекса. Всякий раз при удачном шаге координаты худшей точки заменяется координатами вновь найденной лучшей. При неудачных шагах, т.е. когда не удаётся найти точки, где F меньше, чем уже было достигнуто, предусмотрен поиск второго большего значения, а также сжатие симплекса по текущему направлению и его редукция – уменьшение всех сторон многогранника. В целом, по мере продвижения к минимуму F, многогранник изменяет свою конфигурацию, приспосабливаясь к топологии гиперповерхности ЦФ, а в окрестностях самого минимума уменьшает свой объём до некоторой заданной предельной величины ε . Когда это происходит, считается, что минимум F найден. Более детально алгоритм метода и программы представлен в виде блок-схемы на рис. 1.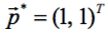 представляет собой узкий искривлённый овраг. Задача минимизации овражистых функций особенно затруднительна. Поэтому функцию Розенброка обычно используют как тестовую задачу в оценках эффективности тех или иных методов минимизации. Записываем процедуру вычисления ЦФ в виде (В программе по умолчанию Sub OF( ) записана в более общем виде.):
представляет собой узкий искривлённый овраг. Задача минимизации овражистых функций особенно затруднительна. Поэтому функцию Розенброка обычно используют как тестовую задачу в оценках эффективности тех или иных методов минимизации. Записываем процедуру вычисления ЦФ в виде (В программе по умолчанию Sub OF( ) записана в более общем виде.):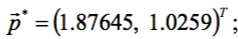 i1 =102. Открываем вкладку "МНК" и просматриваем результат подгонки регрессии.
i1 =102. Открываем вкладку "МНК" и просматриваем результат подгонки регрессии.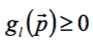 нарушено, и равен 0 в противном случае. Решение задачи сводится к минимизации штрафной функции (ШФ) вида
нарушено, и равен 0 в противном случае. Решение задачи сводится к минимизации штрафной функции (ШФ) вида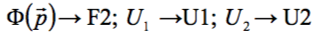 и записываем процедуру в следующем виде:
и записываем процедуру в следующем виде: