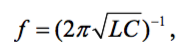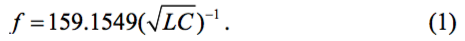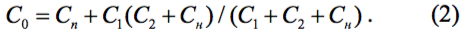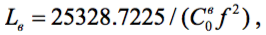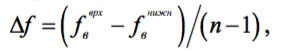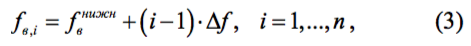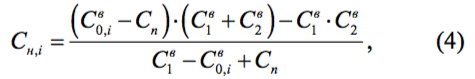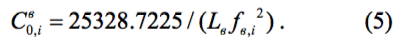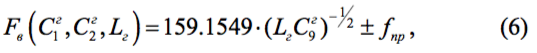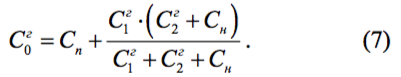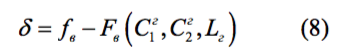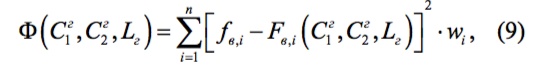QRZ.RU > Каталог схем и документации > Схемы наших читателей > Радиолюбительские конструкции > Подгонка параметров гетеродинного контура к заданному диапазону по методу наименьших квадратов
Подгонка параметров гетеродинного контура к заданному диапазону по методу наименьших квадратов
Новый вариант расчёта сопряжения гетеродинного контура, Oscillator Padding
В предыдущей работе нами был рассмотрен вариант решения задачи сопряжения гетеродинного контура методом наименьших квадратов (МНК), использованным в качестве средства решения 3-х нелинейных уравнений с тремя неизвестными. Логичным продолжением подхода явилось приложение МНК к решению той же задачи в более широкой и универсальной постановке. А именно: отыскать такие параметры гетеродинного контура при заданных параметрах входного контура (селектора), чтобы при синхронной перестройке обоих контуров получалось бы наилучшее (в смысле достижения минимальных невязок частот) сопряжение контуров на всём заданном диапазоне. Разработан алгоритм, который минимизирует сумму квадратов невязок частот по дискретной сетке. При этом автоматически определяются и точки сопряжения, так что отпадает необходимость задавать их заранее из каких бы то ни было соображений. Программа, как и её предшественница, написана на языке Excel Visual Basic в виде макросов. Опубликована автором в сети Интернет для свободного пользования.
I. Суть метода
Чтобы облегчить читателю и пользователю понимание алгоритма решения задачи, уместно повторить кое-что из того, что было уже описано в предыдущей статье [1].
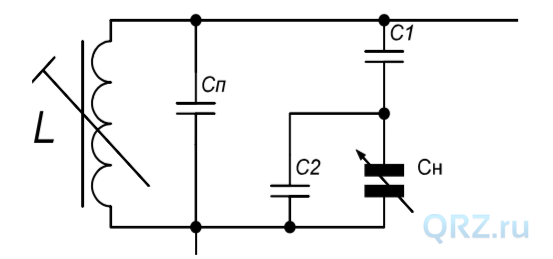
Имеется 2 колебательных контура – входной (УВЧ, селектора, смесителя) и гетеродинный, в состав каждого из которых входит катушка индуктивности, L; ёмкость монтажа суммарно с собственной ёмкостью катушки, Cп; конденсатор настройки Сн и два конденсатора растяжки диапазона, С1 и С2 (см. рис.1).
Рис.1. Общая схема колебательного контура.
1о. Исходные данные:
- Lв – индуктивность входного контура, мкГн,
- ёмкости Сп обоих контуров (одинаковые), пФ
- минимальная и максимальная ёмкости конденсатора настройки (конденсатора переменной ёмкости, КПЕ) - Cнmin Cнmax (для обоих контуров одинаковые), пФ
- граничные частоты диапазона входного контура: fвниж, fвврх, мГц
- кроме того, заданы: промежуточная частота преобразования, fпр, мГц и тип настройки гетеродина (нижняя или верхняя настройка).
2о. Требуется найти (вычислить):
- ёмкости С1в, С2в, конденсаторов растяжки входного контура (1-ый этап расчёта);
- ёмкости С1г, С2г, конденсаторов растяжки и индуктивность Lг гетеродинного контура (2-й этап).
- Определить точки (частоты) точного сопряжения контуров (заключительный этап).
Алгоритм решения данной задачи (за исключением последнего пункта) ранее сводился к следующему.
Задаётся независимо либо вычисляются индуктивность входного контура. Вычисляется полная ёмкость входного контура на границах диапазона. Алгебраически находятся ёмкости конденсаторов растяжки входного контура и значения ёмкости конденсатора настройки (КПЕ) в трёх точках сопряжения диапазона, частоты которых должны быть заданы. Переносятся частоты сопряжения на контур гетеродина путём добавления к ним или вычитания из них значения промежуточной частоты. Параметры Lг, С1г, С2г, гетеродинного контура вычисляются путём совместного решения уравнения в 3-х точках (для 3-х частот) сопряжения гетеродинного контура.
В новом варианте алгоритма сохраняется в неизменном виде этап расчёта параметров входного контура.
II. Основное уравнение для частоты колебательного контура
Частота колебательного контура связана с ёго индуктивностью и ёмкостью соотношением:
где частота задаётся в герцах, индуктивность - в генри, а ёмкость - в фарадах. Если частоту выражать в мГц, индуктивность в мкГн, а ёмкость в пФ, то формула принимает вид:
Полная ёмкость контура, изображённого на рис.1, задаётся формулой:
В дальнейшем при нахождении величин индуктивности и ёмкостей конденсаторов растяжки гетеродинного контура подгонкой невязок частот по МНК, в отличие от ранее рассмотренного алгоритма, уравнение (1) не подвергается преобразованиям.
III. Расчёт ёмкостей конденсаторов растяжки входного контура
Границы диапазона входного контура fвниж, fвврх должны быть заданы. Если исходным параметром является желаемая полная ёмкость входного контура, С0в, на одной из границ диапазона, находится его индуктивность
Где f – частота на соответствующей границе. Как и ранее, значение Lв может быть задано независимо из иных соображений, например, имеется готовая катушка подходящей индуктивности.
По индуктивности и частоте другой границы диапазона вычисляется полная ёмкость входного контура на 2-й границе. Получаются 2 величины: C0min и C0max . Верхние индексы относятся к высокочастотной и низкочастотной границам диапазона, соответственно.
Применяя формулу (2) к границам диапазона входного контура, получаем 2 уравнения для расчёта емкостей C1, C2 (детали см. в статье [1]). Предусмотрен вариант, когда последовательная ёмкость отсутствует, что бывает в случае большого перекрытия диапазона (ДВ, СВ) или когда максимальная ёмкость КПЕ невелика. При этом расчёты упрощаются, а величина Lв определяется однозначно.
После того, как ёмкости конденсаторов растяжки С1г, С2г, вычислены, м.б. найдена ёмкость КПЕ в любой точке диапазона.
Т.о. первый этап решения задачи остаётся прежним. Теперь, когда известны все необходимые параметры входного контура, необходимо определить соответствующие параметры контура гетеродина.
IV. Определение частот сопряжения контуров
Таковой этап отсутствует – частоты точного сопряжения контуров находятся автоматически путём минимизации невязок сопряжения.
V. Алгоритм подгонки сопряжения по диапазону
10. Подготовительные вычисления – формирование рабочих массивов.
Для вычисления невязок настроек контуров по всему заданному диапазону, последний разбивается на равные промежутки,
где n – заданное число точек дискретной сетки диапазона, в которых будут вычисляться невязки сопряжения. Нами выбрано n = 20, что вполне достаточно. Частоты вычисляются по формуле:
и записываются в соответствующий массив. Далее формируется массив значений ёмкости КПЕ в заданных точках:
где значения полной ёмкости входного контура, Cв0,i, рассчитываются по формуле
20. Формулировка функции-модели и целевой функции.
Искомыми величинами, или по терминологии МНК – оценочными параметрами являются С1г, С2г и Lг. Функцией данных параметров будет фактическая частота настройки приёмного устройства (не путать с частотой настройки входного контура fв !):
где полная ёмкость гетеродинного контура есть, в свою очередь, функция искомых параметров С1г, С2г:
Знак плюс в (6) берётся при нижней настройке гетеродина. По терминологии МНК соотношение (6) совокупно с (7) называется функцией-моделью.
Разность
есть невязка частоты (иначе - отклонение, расстройка) входного контура от фактически принимаемой частоты. Именно совокупность невязок частот, вычисленных в точках дискретной сетки (3) подлежит минимизации. По правилам математической статистики, минимизироваться должны не сами отклонения, а сумма их квадратов, т.е функционал или целевая функция:
где Fв,i (С1г, С2г и Lг) задана формулой (6) с учётом соотношения (7); величины wi представляют собой статистические веса невязок, о выборе которых будет сказано ниже. Совокупность искомых параметров, отвечающих минимуму функционала (9) называются МНК-оценками параметров или просто оценками. Это величины статистические и характеризуются также точностью и достоверностью оценивания, для чего служат их среднеквадратичные ошибки и доверительные интервалы.
Нами использован алгоритм минимизации функционала (9) нелинейный МНК в варианте Гаусса-Зайделя (т.н. метод линеаризации модели) с введением гасящих множителей. Описывать его здесь подробно нет возможности, однако необходимо сделать ряд важных замечаний. Процедура эта – итерационная, т.е. требует задания некоторых начальных оценок параметров, после чего вычисляются поправки к ним. При этом сильно нелинейная функция-модель (6)1 разлагается в ряд Тэйлора относительно поправок, где сохраняются только линейные члены. Таким образом, расчёты сводятся к линейным операциям с матрицами. Однако сходимость итерационного процесса обеспечивается не всегда, т.к. необходимым условием сходимости является задание начального приближения возможно ближе к искомому минимуму (9). Если это условие не выполнено, возможна расходимость процесса и даже аварийная остановка программы, например, когда подкоренное выражение в (6) становится отрицательным или равным нулю. Введение гасящих множителей к поправкам часто даёт возможность вернуть процесс в область сходимости, но не всегда. Поэтому вопросу выбора начальных оценок уделено особое внимание.
Алгоритм выбора начальных оценок в словесном выражении сводится к следующему. Полагается, что полная минимальная ёмкость гетеродинного контура равна таковой же входного контура (что, как правило, приближённо так и бывает). По максимальной частоте гетеродина вычисляется начальная оценка индуктивности, потом вычисляется полная ёмкость контура на минимальной частоте. По двум значениям полной ёмкости вычисляются начальные оценки ёмкостей конденсаторов растяжки, как это было описано ранее [1]. При таком задании начальных оценок параметров процедура МНК показывает хорошую сходимость.
О выборе статистических весов. Поскольку полоса пропускания контура пропорциональна его резонансной частоте, то допуск к невязкам должен быть также пропорционален частоте, отсюда принято, что вес тем больше, чем меньше частота:
Конечный результат мало зависит от выбора весов (их можно было бы взять равными 1), но при выборе (10) подгонка в длинноволновой части диапазона, где требования к сопряжению должна быть выше, оказывается несколько более точной.
Заключительный этап расчёта состоит в поиске частот точного сопряжения контуров. Для этого производится поиск по сетке частот пар смежных оценок невязки, которые имеют противоположные знаки. Далее применяется обычная процедура линейной интерполяции к нулевому значению невязки. Практика расчётов показала, что всегда искомых точек оказывается три.
Перейдём к описанию пользовательского интерфейса готовой программы.
V. Программная часть
Как и её предшественница [2], программа написана на языке Basic в среде VBA (Visual Basic for Applications). Проделать следующее:
- Скачать файл программы oscillator_padding_fullfit.xls, пройдя по ссылке [3].
- Открыть приложение Excel, не открывая скачанного файла.
- Т.к. программа является макросами, необходимо снизить уровень безопасности приложения, для чего войти в основном меню по пути: Сервис > Макрос > Безопасность; на открывшейся вкладке выбрать средний уровень безопасности.
- Запустить файл программы и в открывшемся окне предупреждения системы безопасности выбрать «Не отключать макросы». Появится главное окно программы – «Данные».
Необходимо выбрать способ задания индуктивности входного контура (Lentr), отметив нужный вариант значком * в табличке справа. Обязательными данными являются: границы диапазона (Fmin, Fmax), собственная плюс монтажная ёмкость входного контура (Cm), минимальная и максимальная ёмкости КПЕ (Ctmin, Ctmax), тип настройки гетеродина в ячейке B25 (ввести слова «верхняя» или «нижняя», без кавычек) и значение промежуточной частоты (Fint) в ячейку B26.
Хотя программа довольно устойчива к начальным данным, но, как и в предыдущей программе, выбираемые значения исходных величин не должны быть абсурдными. В частности, это относится к частотам диапазона, который не должен быть чрезмерно широк, так что не может быть перекрыт выбранным КПЕ, равно и слишком узким, когда задача может стать вырожденной (пока такой случай ещё не встретился). Вариант «Рассчитывается по Fmin,max (при отсутствии С1)» относится к нерастянутым диапазонам ДВ и СВ, а также к другим диапазонам, если используется КПЕ небольшой ёмкости. Обычно он необходим, когда получаются очень большие значения C1 (более 10000 пФ) или меньше нуля. Если же получаются отрицательными значения C2, то велика начальная ёмкость контура для заданной Fmin. Возможны иные варианты ограничений, в которых пользователь может разобраться самостоятельно.
Запускается программа нажатием <ctrl+s> при англоязычной раскладке клавиатуры. Программа заполняет все необходимые ячейки таблицы, за исключением строк 17-19 и трёх нижних2. Следует внимательно ознакомиться с результатом и на появившемся сообщении «Готово» щёлкнуть «ОК». Откроется окно программы «МНК», где ничего, как правило, менять не нужно. Не следует также что-либо менять на служебных вкладках «Процесс» и «Параметры». Запустить второй и третий этап вычислений следует нажатием <ctrl+f>. После щелчка на «ОК» в окошке «Готово» данные расчёта параметров гетеродинного контура и частоты точного сопряжения заносятся в соответствующие ячейки листа «Данные». Для того, чтобы посмотреть результаты подгонки, надо вернуться на вкладку «МНК». Помимо рабочих массивов исходных данных будут видны оценки параметров, их квадратичные ошибки и полуинтервалы при доверительной вероятности 95%. Ниже следует регрессионная таблица – целевые и достигнутые значения частот по заданной сетке, а также невязки. Ещё ниже – результат поиска частот точного сопряжения.
VI. Примеры
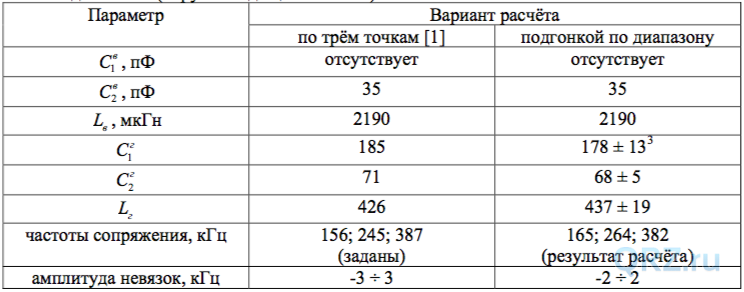
1о. Рассмотрим расчёт сопряжения контуров для диапазона ДВ (0,145 – 0,415 мГц). Имеется КПЕ от 12 до 495 пФ. Собственная ёмкость, включая ёмкость монтажа равна 20 пФ. Значение ПЧ – 465 кГц, настройка гетеродина верхняя. Выбираем вариант расчёта «Рассчитывается по Fmin,max (при отсутствии С1)» и запускаем 1-ый макрос. Получаем в результате параметры входного контура (округлённо): L = 2190 мкГн; С1 - отсутствует; С2 = 35,2 пФ. Запускаем 2-ой макрос и находим параметры контура гетеродина: L = 426 мкГн; С1 = 185 пФ; С2 = 71 пФ.
Сравниваем полученный результат с тем, что был найден подгонкой по трём точкам диапазона (округлено до целых чисел):
Из приведённых данных видно, что МНК-подгонка параметров по сетке частот даёт немного иной результат, хотя интервальные значения накрывают ранее полученные. Несколько различны и частоты точного сопряжения. В целом результат подгонки обеспечивает меньшую амплитуду невязок частот. Кроме того, программа наглядно показывает распределение невязок по диапазону, что весьма удобно.
В заключение следует повторить, что после вычислений и пайки соответствующих схем всё равно так или иначе придётся корректировать найденные параметры. Однако предварительные расчёты сопряжения контуров по программе сильно облегчают их дальнейшую настройку.
С вопросами и замечаниями относительно метода расчёта и работы с программой можно обратиться к автору по эл. почте:
.
ЛИТЕРАТУРА
- Цибанов В.В. Об одном варианте расчёта сопряжения гетеродинного контура. Посещён 08.10.2017.
- URL: http://tsibanoff.narod.ru/radio/oscillator_padding-3pointfit.xls Посещён 08.10.2017.
- URL: http://tsibanoff.narod.ru/radio/oscillator_padding-fullfit.xls
1 Нелинейность обусловлена тем, что LC находится в знаменателе и под квадратным корнем, а искомые параметры встречаются в виде произведений и дробей, что приводит к их сильной взаимосвязи.
2 До запуска программы в таблице остаются значения от предыдущих расчётов.
3 95%-ый доверительный интервал.